DearMiku

iOS安全 -- 数据加密

iOS安全
字数统计: 3.3k阅读时长: 13 min
2017/11/19 Share

Base64

base64是一种基于64个可打印字符来表示二进制数据的表示方法.严格来说它只能算作一种编码方式.
Base64编码之所以称为Base64，是因为其使用64个字符来对任意数据进行编码，同理有Base32、Base16编码

作用:

1, 由于某些系统中只能使用ASCII字符。Base64就是用来将非ASCII字符的数据转换成ASCII字符的一种方法.
2, 使用SMTP协议 （Simple Mail Transfer Protocol 简单邮件传输协议）来发送邮件。因为这个协议是基于文本的协议，所以如果邮件中包含一幅图片，我们知道图片的存储格式是二进制数据（binary data），而非文本格式，我们必须将二进制的数据编码成文本格式，这时候Base 64 Encoding就派上用场了.
3, 通过base64将ASCII不可见字符转换为可见字符

使用:

1
2
3
4
5
6
7
8
9
10
11
//编码
- (NSString *)base64EncodedString;{
NSData *data = [self dataUsingEncoding:NSUTF8StringEncoding];
return [data base64EncodedStringWithOptions:0];
}

//解码
- (NSString *)base64DecodedString{
NSData *data = [[NSData alloc]initWithBase64EncodedString:self options:0];
return [[NSString alloc]initWithData:data encoding:NSUTF8StringEncoding];
}

MD5

MD5(消息摘要算法第五版)为计算机安全领域广泛使用的一种散列函数，用以提供消息的完整性保护.

特点:

1、压缩性：任意长度的数据，算出的MD5值长度都是固定的(32摘要)。
2、容易计算：从原数据计算出MD5值很容易。
3、抗修改性：对原数据进行任何改动，哪怕只修改1个字节，所得到的MD5值都有很大区别。
4、强抗碰撞(难逆向)：已知原数据和其MD5值，想找到一个具有相同MD5值的数据（即伪造数据）是非常困难的。

作用

1, 数字签名, 当我们传递敏感信息时,可以为利用MD5+时间戳+盐 为消息添加唯一的数字签名,当服务端获得数据后,用相同算法再次签名.进行比较 若不一致 则数据遭到篡改.
2, 文件验证, 我们在下载文件时,由于复杂的网络环境,我们下载的文件可能会有内容丢失或篡改的可能性.(例如我们从服务器获取的H5文件遭到了JS注入),利用MD5可以有效防止这些事情的发生.

同类算法

SHA-1:

会产生一个160位的消息摘要,SHA-1的安全性在2000年以后已经不被大多数的加密场景所接受。2017年荷兰密码学研究小组CWI和Google正式宣布攻破了SHA-1.

SHA-2:

2001年发布，包括SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。虽然至今尚未出现对SHA-2有效的攻击，它的算法跟SHA-1基本上仍然相似；因此有些人开始发展其他替代的散列算法。

SHA-3:

2015年正式发布，SHA-3并不是要取代SHA-2，因为SHA-2目前并没有出现明显的弱点。由于对MD5出现成功的破解，以及对SHA-0和SHA-1出现理论上破解的方法，NIST感觉需要一个与之前算法不同的，可替换的加密散列算法，也就是现在的SHA-3。

实现

这里是对字符串的散列计算,若对文件则需要先读取文件流再去散列.
需要: import <CommonCrypto/CommonDigest.h>

MD5

1
2
3
4
5
6
- (NSString *)md5String {
    const char *str = self.UTF8String;
    uint8_t buffer[CC_MD5_DIGEST_LENGTH];
    CC_MD5(str, (CC_LONG)strlen(str), buffer);
    return [self stringFromBytes:buffer length:CC_MD5_DIGEST_LENGTH];
}

SHA-1:

1
2
3
4
5
6
7
8
- (NSString *)sha1String {
    const char *str = self.UTF8String;
    uint8_t buffer[CC_SHA1_DIGEST_LENGTH];
    
    CC_SHA1(str, (CC_LONG)strlen(str), buffer);
    
    return [self stringFromBytes:buffer length:CC_SHA1_DIGEST_LENGTH];
}

SHA256:

1
2
3
4
5
6
7
8
- (NSString *)sha256String {
    const char *str = self.UTF8String;
    uint8_t buffer[CC_SHA256_DIGEST_LENGTH];
    
    CC_SHA256(str, (CC_LONG)strlen(str), buffer);
    
    return [self stringFromBytes:buffer length:CC_SHA256_DIGEST_LENGTH];
}

SHA512:

1
2
3
4
5
6
7
8
- (NSString *)sha512String {
    const char *str = self.UTF8String;
    uint8_t buffer[CC_SHA512_DIGEST_LENGTH];
    
    CC_SHA512(str, (CC_LONG)strlen(str), buffer);
    
    return [self stringFromBytes:buffer length:CC_SHA512_DIGEST_LENGTH];
}

SHA3:

需要在github上下载keccak代码包 :https://github.com/gvanas/KeccakCodePackage

大文件的计算:

这里以MD5为例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#define FileHashDefaultChunkSizeForReadingData 4096

- (NSString *)fileMD5Hash {
    //打开一个文件准备读取
    NSFileHandle *fp = [NSFileHandle fileHandleForReadingAtPath:self];
    if (fp == nil) {
    //若路径为文件夹这种的(如:.framework)则会返回Null
        return nil;
    }
    //创建MD5变量
    CC_MD5_CTX hashCtx;
    //初始化MD5变量
    CC_MD5_Init(&hashCtx);
    
    while (YES) {
        @autoreleasepool {
        //读取文件指定长度数据,循环读取避免一次加载到内存过大
            NSData *data = [fp readDataOfLength:FileHashDefaultChunkSizeForReadingData];
            //准备MD5加密,将内容上传
            CC_MD5_Update(&hashCtx, data.bytes, (CC_LONG)data.length);
            
            if (data.length == 0) {
                break;
            }
        }
    }
    //关闭文件
    [fp closeFile];
    
    //创建MD5结果缓冲区
    uint8_t buffer[CC_MD5_DIGEST_LENGTH];
    //将MD5结果写进缓冲区
    CC_MD5_Final(buffer, &hashCtx);
    
    //原始数据转换为字符串
    return [self stringFromBytes:buffer length:CC_MD5_DIGEST_LENGTH];
}

- (NSString *)stringFromBytes:(uint8_t *)bytes length:(int)length {
    NSMutableString *strM = [NSMutableString string];
    
    for (int i = 0; i < length; i++) {
        [strM appendFormat:@"%02x", bytes[i]];
    }
    
    return [strM copy];
}

对于其他的算法文件加密方式也是这样的,它们都是由CommonCrypto库提供的.

HMAC散列计算(加盐)

HMAC是密钥相关的哈希运算消息认证码，HMAC运算利用哈希算法，以一个密钥和一个消息为输入，生成一个消息摘要作为输出。
HMAC算法更象是一种加密算法，它引入了密钥，其安全性已经不完全依赖于所使用的HASH算法,有些类似对称加密,但是是不可逆的那种~.
以MD5为例:

1
2
3
4
5
6
7
8
9
10
11
- (NSString *)hmacMD5StringWithKey:(NSString *)key {
    const char *keyData = key.UTF8String;
    const char *strData = self.UTF8String;
    //切换其他散列函数替换这里(如:CC_SHA256_DIGEST_LENGTH)
    uint8_t buffer[CC_MD5_DIGEST_LENGTH];
        //切换其他散列函数替换这里(如:kCCHmacAlgSHA256)
    CCHmac(kCCHmacAlgMD5, keyData, strlen(keyData), strData, strlen(strData), buffer);
    
   //切换其他散列函数替换这里(如:CC_SHA256_DIGEST_LENGTH)
    return [self stringFromBytes:buffer length:CC_MD5_DIGEST_LENGTH];
}

AES(对称加密)

简介

美国国家标准技术研究所在2001年发布了高级加密标准（AES）。
AES是基于数据块的加密方式，
即，每次处理的数据是一块（16字节），当数据不是16字节的倍数时填充，
这就是所谓的分组密码（区别于基于比特位的流密码），16字节是分组长度。

AES在软件及硬件上都能快速地加解密，相对来说较易于实现，

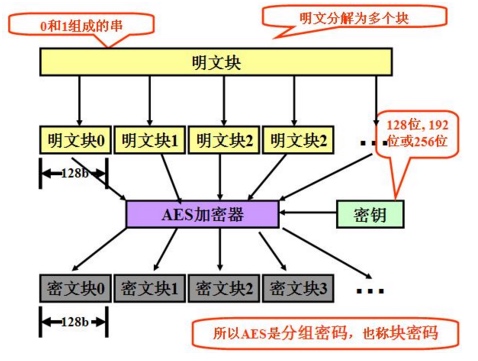
实现

在使用AES时要配置几个加密参数,只有都一致才能使 客户端与服务端 结果一致.

参数配置

密钥长度

key常见的长度有三种：128、192和256 bits

加密模式

AES属于块加密（Block Cipher），块加密中有CBC、ECB、CTR、OFB、CFB等几种工作模式.

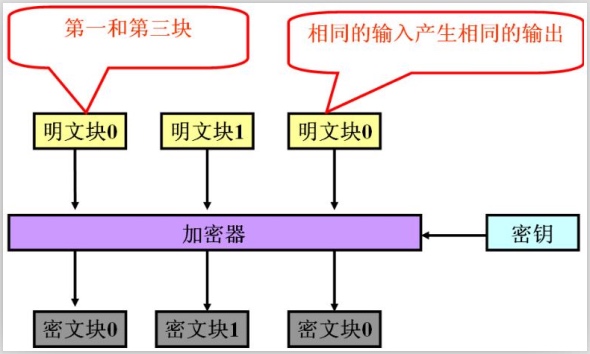
ECB

是一种基础的加密方式,AES默认没收,密文被分割成分组长度相等的块（不足补齐），然后单独一个个加密,一个个输出组成密文.

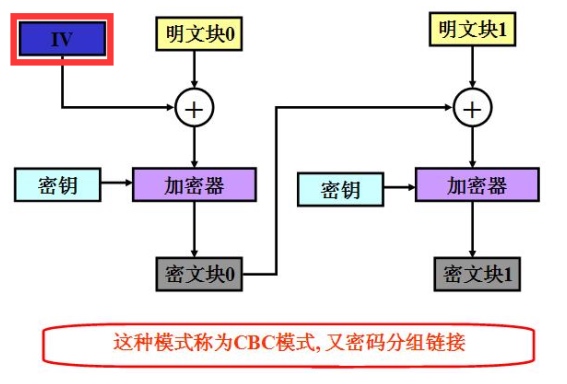
CBC

这个模式是链式的,后一块需要前一块做基础，第一块需要一个需要初始化向量IV做基础.
相同的输入产生不同的输出.
能看到的数据是“明文+IV”或“明文+前一个密文”的乱码，所以能隐藏明文.

所以加密/解密 需要: 明文/密文 + 秘钥 + 初始向量参数

填充方式

因为AES的算法是把明文分组再处理的,他要求每个分组(16字节)是“满”的,即明文长度必须被16字节整除.

所以明文最后不足的16字节的要先进行数据填充,把不足16字节的最后一组补成16字节.

CFB,OFB和CTR模式由于与key进行加密操作的是上一块加密后的密文,因此不需要对最后一段明文进行填充.
在iOS SDK中提供了PKCS7Padding.

初始向量

正如在CBC模式哪里介绍的,开始加密时,从哪里开始就是初始向量,如不设置则系统默认为0;

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
NSString *const kInitVector = @"初始向量";

size_t const kKeySize = kCCKeySizeAES256;//秘钥长度

+ (NSData *)encryptAES:(NSData *)content key:(NSString *)key {
    
    NSData *contentData = content;
    NSUInteger dataLength = contentData.length;
    
    //设置加密秘钥,因C字符串结束符为'\0' 所以大小+1
    char keyPtr[kKeySize + 1];
    memset(keyPtr, 0, sizeof(keyPtr));
    //应确保大小小于等于16个字节.
    [key getCString:keyPtr maxLength:sizeof(keyPtr) encoding:NSUTF8StringEncoding];
    
    //密文长度 = 明文长度+秘钥长度
    size_t encryptSize = dataLength + kCCBlockSizeAES128;
    void *encryptedBytes = malloc(encryptSize);
    
    //密文接受指针
    size_t actualOutSize = 0;
    
    //初始向量
    NSData *initVector = [kInitVector dataUsingEncoding:NSUTF8StringEncoding];
    
    CCCryptorStatus cryptStatus = CCCrypt(kCCEncrypt,               //是加密还是解密
                                          kCCAlgorithmAES,          //加密/解密方式
                                          kCCOptionPKCS7Padding,    //PKCS7Padding
                                          keyPtr,                   //秘钥
                                          kKeySize,                 //秘钥大小
                                          initVector.bytes,         //初始向量
                                          contentData.bytes,        //明文/密文
                                          dataLength,               //明文/密文大小
                                          encryptedBytes,           //结果: 密文/明文缓冲区
                                          encryptSize,              //结果: 密文/明文大小
                                          &actualOutSize);          //结果指针
    
    if (cryptStatus == kCCSuccess) {
        // 成功
        return [NSData dataWithBytesNoCopy:encryptedBytes length:actualOutSize];
    }
    //释放
    free(encryptedBytes);
    return nil;
}

RSA

原理

数学基础

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质的数.计算这个值的函数为 欧拉函数: 如: φ(8) = 4.

若n为质数 则: φ(n) = n-1 原理3
若n为质数的n次方 则: φ(p^k) = p^k - p^(k-1)
若n为两个互质整数之积 则: φ(p1 p2) = φ(p1)φ(p2) 原理1
若正整数 a和n互质 则: a^φ(n) 被n除的余数为1 则: a^φ(n) %n=1 欧拉定理
若正整数a和质数p互质 则: a^p-1 %p=1 //费马小定理
若正整数a和n互质,则一定可以找到正整数b 使: ab%n=1, b为a的模反元素. *原理2

秘钥生成

1, 随机生成两个不等质数p和q 如 p=61 q=53

2, 求出pq乘积n n=p q= 6153=3233.

这里n的长度即为,秘钥长度,如3233为二进制12位,RSA秘钥一般为1024位.

3, 计算φ(n)

根据 原理1 φ(n) = φ(p)φ(q) = (p-1)(q-1) = 3120

4, 随机选择一个整数e 条件为 1<e<φ(n) 且 e与φ(n)互质

假如选择 17

5, 获取e对于φ(n)的模反元素d

ed%φ(n)=1 —> ed -1 = kφ(n) —> 17d + 3120k = 1
通过扩展欧几里德算法 可得到一组整数解 d=2753 k=-15

6, 这里 n和e 为公钥 n和d 为私钥

加密(此处为公钥加密 n e)

对明文信息m 加密 注意:m为正整数,且m须小于n

m^e % n = c 这里的c就是加密后得到的密文
65^17 % 3233 = 2790 这里2790就是加密后的密文

解密(n d)

解密原理

解密规则为: c^d %n = m

因为加密过程为: m^e % n = c —> c = m^e - kn
若想证明解密规则成立 则等同于证明 (m^e - kn)^d % n = m 成立

(m^e - kn)^d % n = m —> m^ed % n = m

由于在制作公私钥 的第5步 所以:

ed%φ(n)=1 —> ed = hφ(n)+1

将ed代入须证明公式:

m^ed % n = m —> m^hφ(n)+1 % n = m

若m n 互质

m^hφ(n)+1 % n = m —> ((m^φ(n))^h * m) % n = m

由于欧拉定理 m^φ(n) %n=1可得
((m^φ(n))^h m) % n = m —> (1^h m) % n = m 则解密公式成立

若m n 不互质

因为制作公私钥 的第1步 n = p * q

因为加密方法 m^e % n = c , 且因 m<n(这里是在制作时要求的) 所以 c肯定不为0 由此可得 m 与 n 不为互质关系.

由于 n = pq 且 pq互质 所以 n有且只有 p q 两个因子. 然而 m n有公因子 所以 m n 的公因子 必定为 q或p的整数倍. 所以 m = kp 或 kq

以 m=kp为例 因为上面描述的关系 m m与q互质

由欧拉定理得:
m^φ(q) % q = 1 —> 由于q为质数 —> m^q-1 % q = 1 –> (kp)^q-1 % q = 1

因为 k与q互质 p与q互质 –> ((kp)^q-1 * kp)%q = kp

进一步可以确定该式成立: (((kp)^h(p-1)(q-1)) * kp)%q = kp 因为p为质数 h为任一整数

由原理1和原理3(((kp)^h(p-1)(q-1)) * kp)%q = kp —> (kp)^hφ(n)+1 %q=kp

由于 ed%φ(n)=1,且m=kp 所以将h匹配为合适的值得 (kp)^ed %q = kp —> (m)^ed = tq +m t为整数.

两侧同除m得: (m)^ed-1 = tq/m +1 由于ed为整数,m为整数 故tq/m为整数. 因q与m互质 所以t为m的整数倍 –> t = yp —> m^ed = yn+m —> m^ed % n = m

由于加密方式 m^e % n = c —> c^d % n = m

安全性讨论

若想破解RSA 则需要在已知 n e的情况下 求 d 因为

因为 ed%φ(n)=1 所以需知道 φ(n)
因为 φ(n) = (p-1)(q-1) 所以需求得 qp
因为 qp=n 所以得将n因式分解

而因式分解是十分困难的 特别是对于 特大整数的因式分解. 由于 名文m 需小于 秘钥长度n 所以常用来加密 对称加密的秘钥.

iOS实现

参考链接:iOS中使用RSA加密
在iOS中使用RSA加密解密 需要使用到.der 和 .p12 后缀格式文件.

.p12 格式文件是用来加密的 私钥
.der 格式文件用来解密的 公钥

添加动态库 Security.framework

具体实现太长,我汇总了一个类 感兴趣可以下下来看看 如果帮到你 点个Star鼓励一蛤~github链接

原文作者：杨尚达

原文链接：http://yoursite.com/2017/11/19/iOS安全 -- 数据加密/

发表日期：November 19th 2017, 7:31:29 pm

更新日期：December 13th 2017, 8:58:37 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Base64
    1. 1.1. 作用:
    2. 1.2. 使用:
  2. 2. MD5
    1. 2.1. 特点:
    2. 2.2. 作用
    3. 2.3. 同类算法
    4. 2.4. 实现
      1. 2.4.1. MD5
      2. 2.4.2. SHA-1:
      3. 2.4.3. SHA256:
      4. 2.4.4. SHA512:
      5. 2.4.5. SHA3:
      6. 2.4.6. 大文件的计算:
      7. 2.4.7. HMAC散列计算(加盐)
  3. 3. AES(对称加密)
    1. 3.1. 简介
    2. 3.2. 实现
      1. 3.2.1. 参数配置
        1. 3.2.1.1. 密钥长度
        2. 3.2.1.2. 加密模式
          1. 3.2.1.2.1. ECB
          2. 3.2.1.2.2. CBC
        3. 3.2.1.3. 填充方式
        4. 3.2.1.4. 初始向量
      2. 3.2.2. 代码
  4. 4. RSA
    1. 4.1. 原理
      1. 4.1.1. 数学基础
      2. 4.1.2. 秘钥生成
      3. 4.1.3. 加密(此处为公钥加密 n e)
      4. 4.1.4. 解密(n d)
        1. 4.1.4.1. 解密原理
          1. 4.1.4.1.1. 若m n 互质
          2. 4.1.4.1.2. 若m n 不互质
      5. 4.1.5. 安全性讨论
    2. 4.2. iOS实现
Total : 31
2019
2018
2017
iOS网络 Python Mac开发 第三方框架学习 MySQL P2P Opengl ES iOS安全 iOS基础 iOS效率 开源 生产工具 计算机基础